Introduction
Markov chains are a really interesting statistical tool that can be used to model phenomena in a wide range of fields. They can be found in the natural sciences, information theory, economics, games, and more. They are commonly used to model stochastic processes, or more informally, a set of random variables that change over time. Markov chains can be expressed in several different notations, though the most common, and the one that will be used for this post, will be as a weighted directed graph. An example of a Markov chain is shown below:
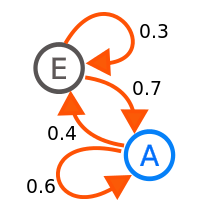
This Markov chain has two states, denoted by vertices A and E. Each vertex has incoming and outgoing edges, with each edge having a weight value associated with it corresponding to a probability. For example, starting at state A, there is a 40% chance that the next state will be a transition to state E, and a 60% chance that the next state will stay at A. In order to be a Markov chain, the sum of all outgoing edge weights for every node must add up to 1.0 (100%); if we start at a vertex then we have to make a move somewhere in the next step. The other characteristic is that the future only depends on the immediate past: the probability of transitioning to any particular state is dependent solely on the current state, and not on the sequence of state transitions that happened earlier in time. This gives Markov chains the property of being memoryless.
An example
Despite initially seeming complex, creating a basic Markov chain is pretty straightforward. To create the Markov chain, we need to take the input corpus of text and build a directed graph for it. Each vertex in this graph will correspond to a word, and each vertex will have an edge to an adjacent word. Then, to generate a sentence, we can start with a seed word and perform a random walk starting from the seed word up to a specified length.
As an example, look at the following input text:
A paragraph is a self-contained unit of discourse in writing dealing with a particular point or idea. A paragraph consists of one or more sentences. Though not required by the syntax of any language, paragraphs are usually an expected part of formal writing, used to organize longer prose.
To quickly build a directed graph for this, we can utilize a dictionary. Each key in this dictionary will correspond to a vertex, and the list of values for this key will correspond to edges.
{
'a': ['paragraph', 'self-contained', 'particular', 'paragraph'],
'paragraph': ['is', 'consists'],
'is': ['a'],
'self-contained': ['unit'],
'unit': ['of'],
'of': ['discourse', 'one', 'any', 'formal'],
'discourse': ['in'],
'in': ['writing'],
'writing': ['dealing', 'used'],
'dealing': ['with'],
'with': ['a'],
'particular': ['point'],
'point': ['or'],
'or': ['idea', 'more'],
...
}If we look at the dictionary output and reference the original text, we can better understand how it was built. Looking through the text, for every instance where the word a appears, we store its adjacent word. In this case, there were four places where the word a had an adjacent word:
A paragraph is …
a self-contained unit of discourse …
a particular point or idea …
A paragraph consists of one ….
The same logic follows for paragraph, is, and so on. One important thing to note is that the keys are not case sensitive. The occurrence of A and a in the text are treated as being the same word, which is a behavior that we desire. Aside from capitalization, there are also other features from the text that we would like to transform or filter out: punctuation marks, newlines, extraneous spaces, and non-printable characters should be removed from the text before the Markov chain is built. Doing this normalization process will help make the output look more consistent with how real sentences are structured.
Another important feature to notice is that there are repetitions: you can see the word paragraph multiple times for the key a. This is done for the simplicity of implementation — we are creating redundant edges from a vertex instead of building and updating a transition matrix. With the redundant approach, we can just randomly select among any edge to transition to and not have to explicitly keep track of probabilities. This has the benefit of making building the model, and generating sentences, easier, since there is no need to build and apply a transition matrix. However, there is the obvious downside of a much greater memory overhead.
Having said that, the code for everything is shown below:
import argparse
import collections
import os.path
import random
import re
import sys
def generate_sentence(markov_table, seed_word, num_words):
if seed_word in markov_table:
sentence = seed_word.capitalize()
for i in range(0, num_words):
next_word = random.choice(markov_table[seed_word])
seed_word = next_word
sentence += " " + seed_word
return sentence
else:
print("Word {} not found in table.".format(seed_word))
def create_markov(normalized_text):
words = normalized_text.split()
markov_table = collections.defaultdict(list)
for current, next in zip(words, words[1:]):
markov_table[current].append(next)
return markov_table
def normalize_text(raw_text):
pattern = re.compile(r"[^a-zA-Z0-9- ]")
normalized_text = pattern.sub("", raw_text.replace("\n", " ")).lower()
normalized_text = " ".join(normalized_text.split())
return normalized_text
def main(args):
if not os.path.exists(args.inputfile):
print("File {} does not exist.".format(args.inputfile))
sys.exit(-1)
with open(args.inputfile, "r", encoding="utf-8") as input_file:
normalized_text = normalize_text(input_file.read())
model = create_markov(normalized_text)
generated_sentence = generate_sentence(model, normalize_text(args.seed), args.numwords)
print(generated_sentence)
if __name__ == "__main__":
parser = argparse.ArgumentParser()
optional = parser._action_groups.pop()
required = parser.add_argument_group("required arguments")
required.add_argument("-i", "--inputfile", required=True)
required.add_argument("-s", "--seed", required=True)
optional.add_argument("-n", "--numwords", nargs="?", default=int(30))
parser._action_groups.append(optional)
args = parser.parse_args()
main(args)This script takes an input file, a seed word, and an optional max number of words to generate. It will then open and read the input file, normalize the text, build the Markov chain, and generate a sentence. Running this script against a larger corpus of text, such as the first two chapters of Hackers, Heroes of the Computer Revolution can produce some pretty funny output:
His group that had a rainbow-colored explosion of an officially sanctioned user would be bummed among the kluge room along with
A sort of the artistry with owl-like glasses and for your writing systems programs–the software so it just as the computer did the clubroom
This particular keypunch machines and the best source the execution of certain students like a person to give out and print it
Having learned a bit more about Markov chains, the next part will cover the steps needed to build a Discord bot that utilizes them to generate chat messages.